Numération

1. Stockage et communication

1.1. Stockage

Un ordinateur ne traite que des données numériques. Dans sa mémoire, l’information n’est qu’une suite interminable de choix binaires (interprétés comme 0/1, vrai/faux, on/off, etc.), appelés bit (binary digit), et regroupés par paquet de 8 appelé octet (byte). L’octet est donc l’unité élémentaire de codage de l’information. Il peut être vu comme un entier compris entre 0 et 255 (2⁸). A partir de l’octet sont dérivées les unités usuelles que sont le kilo-octet (Ko, 10³ o), le méga-octet (Mo, 10⁶ o), le giga-octet (Go, 10⁹ o), le tera-octet (To, 10¹² o) et le peta-octet (Po, 10¹⁵ o).

Le CPU de l’ordinateur est l’endroit où sont réalisés les calculs. Les données transitent entre la mémoire (où elles sont stockées) et le CPU (où elles sont traitées). Dans le CPU, le stockage se fait dans des registres (en petit nombre), destinés à conserver temporairement les opérandes et le résultat des opérations arithmétiques à réaliser. La taille d’un registre est appellée mot (ou mot machine). Sur une architecture 32 bits, il est de 4 octets, et sur une architecture 64 bits, il est de 8. Il était de 2 octets dans les ordinateurs 16 bits des années 80.

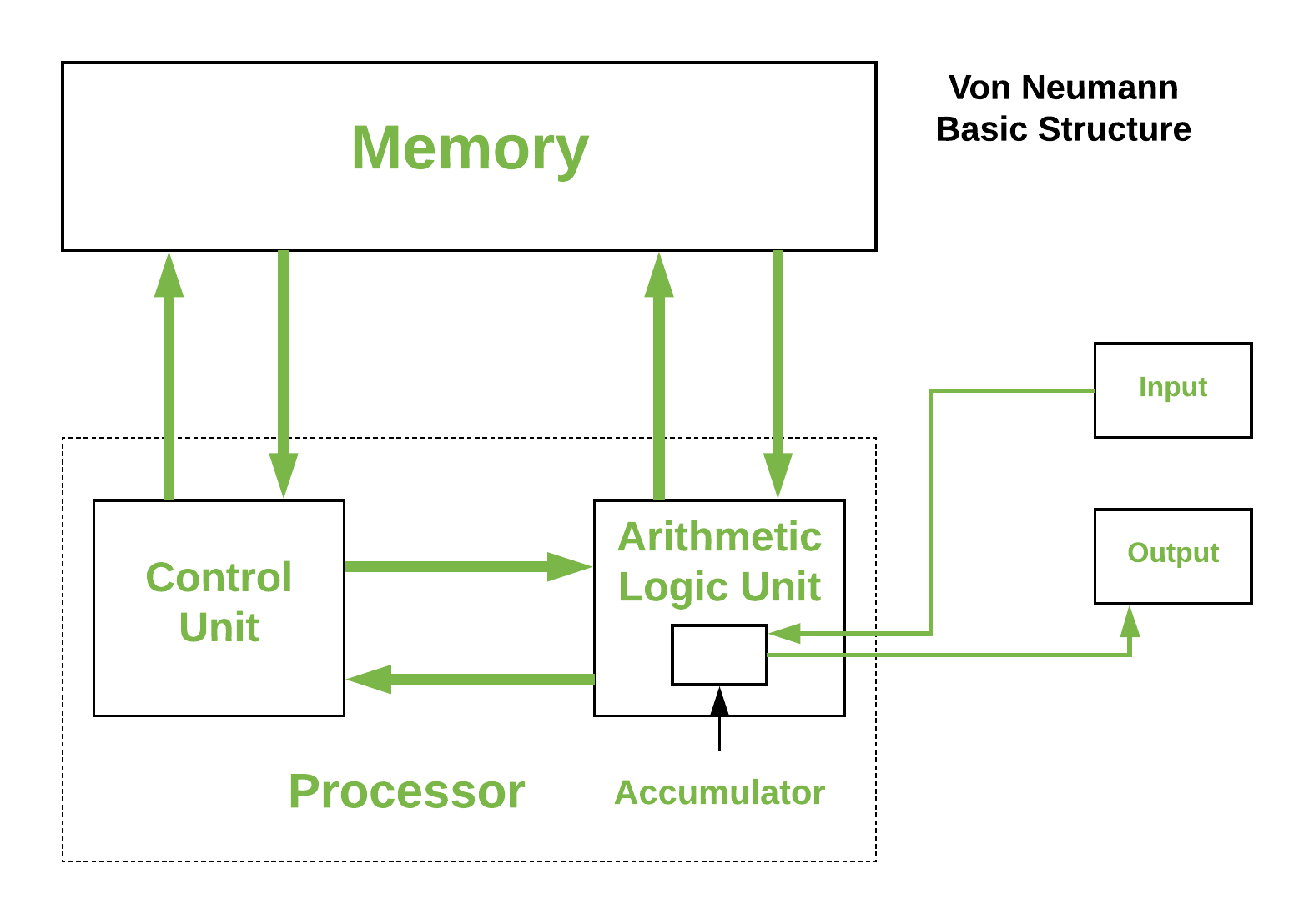
Une donnée en mémoire de 2 octets o1-o2 recopiée dans un registre 16 bits peut donner à l’arrivée, suivant le matériel, soit o1-o2, soit o2-o1. Cette caractéristique s’appelle boutisme en français, endianness en anglais. Elle intervient à chaque fois que des données binaires transitent entre 2 composants électroniques, par exemple lorsque qu’un programme récupère des données numériques d’un appareil de mesure (capteur, sismographe, séquenceur du génôme…).

Par exemple, les processeurs Intel x86 et AMD64/x86-64 sont petit boutistes (little-indian), le processeur Motorola 68000 est gros boutiste (big-indian). Il existe des processeurs (PowerPC, Alpha) où cela est configurable (bi-indian).

1.2. Communication

Les communications informatiques sont des échanges d’octets. Sur de courtes distances, le transfert peut s’effectuer octets par octets. On parle alors de liaison parallèle, dans laquelle les 8 bits de chaque octet circulent en parallèle sur 8 canaux en même temps :

Sur de plus grandes distances (cas des réseaux), le transfert des octets se fait bit par bit , à la queue leu-leu. On parle alors de liaison série. C’est pourquoi le débit d’une liaison série, par exemple une liaison réseau, s’exprime en bits par seconde (avec les mêmes unités : b/s, Kb/s, Mb/s, Gb/s).

1.3. Langage de bas niveau vs langage de haut niveau

Les éléments d’informations que sont les octets sont aggrégés pour former des données structurées. Dans les langages de programmation de bas niveaux d’abstraction (comme les langages C ou Fortran), les types scalaires (entier, flottant, booléan) collent de près à l’architecture matérielle. Par exemple, les entiers correspondent à ce que le CPU est capable de traiter nativement, c’est-à-dire 4 octets sur une architecture 32 bits, ou bien 8 octets sur une architecture 64 bits. Les programmes codés dans ses langages de bas niveau sont donc rapides, puisqu’ils manipulent des données formatées pour correspondre exactement aux caractéristiques physiques du matériel.

Quand le niveau d’abstraction s’élève (comme avec Java ou Python), les types de données s’éloignent de la réalité, et deviennent des constructions de l’esprit. Les programmes sont alors plus lents, car une couche logicielle s’intercale entre ce que le programmeur écrit dans son code et ce qu’exécute le CPU de la machine. Par exemple, le type dictionnaire de Python n’a pas de correspondance physique ni dans le CPU, ni dans la mémoire de la machine. Les opérations effectuées sur un dictionnaire demandent à être traduite en des instructions manipulant des données réelles, d’où une perte d’efficacité. Même le type entier de Python est très éloigné de la représentation des entiers dans le CPU, ce qui explique en partie les temps de calcul médiocres des programmes Python.

Les lignes suivantes suffisent à s’en convaincre :

import sys
sys.getsizeof(0)                # 24 octets
sys.getsizeof(100000)           # 28  octets
sys.getsizeof(1000000000000000) # 32 octets
sys.getsizeof(int)              # 424 octets

2. Binaire et hexadécimal

Habituellement, dans le code d’un programme, les entiers sont exprimés en base 10. Mais lorsque l’agencement des bits revêt une importance dans la compréhension des choses, il est pratique de pouvoir utiliser la base 2.

Soit le programme :

for n in range(0,128):
        print(f"{n & 31}", end=" ")

qui sort :

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

Pour comprendre le résultat, mieux vaut exprimer 31 en binaire :

en décimal: 31
en binaire: 00011111

Sous cette forme, il est clair qu’un ET (&) laisse les 5 bits de poids faibles inchangés et met les autres à 0. Il aurait été plus clair d’écrire :

for n in range(0,128):
  print(f"{n & 0b00011111}", end=" ")

Mais le binaire est fastidieux à écrire. L’hexadécimal (base 16) permet d’en compacter l’écriture, en groupant les bits 4 par 4. Les 16 chiffres de l’hexadécimal sont 0123456789ABCDEF.

Le programme aurait pu s’écrire :

for n in range(0,128):
  print(f"{n & 0x1F}", end=" ")

3. Numération et représentation en Python

3.1. Constantes entières

Dans un code Python, un entier littéral commençant par 0x ou 0X est une valeur hexadécimale, s’il commence par 0b ou 0B, c’est une valeur binaire, sinon c’est un décimal :

0xF0       # 1111 0000 en binaire, 240 en décimal
0xFFFF     # 1111 1111 1111 1111 en binaire, 65535 en décimal
0b11111111      # FF en hexa, 255 en décimal
0b_0001_0000    # 10 en hexa, 16 en décimal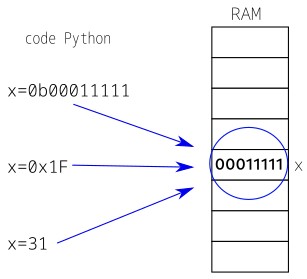

Figure 1. expression d’un littéral entier en différentes bases

3.2. Représentation textuelle d’un entier

Rendre un entier humainement lisible suppose de le transformer en une suite de caractères, représentant chacun 1 chiffre de l’entier. Par exemple, l’entier 123 est représenté en mémoire comme 1111011. print(123) convertit donc 1111011 en une chaîne de 3 caractères '1','2' et '3'. De même, print(0b11) écrit le caractère '3', et print(0xff) écrit les 3 caractères '2', '5' et '5'.

print sort donc la représentation en base 10 de l’entier spécifié, quelle que soit la base dans laquelle l’entier est exprimé dans le code source. Les f-strings permettent de spécifier la base dans laquelle on souhaite l’écrire :

Inversement, on peut obtenir un entier à partir d’une chaîne de caractères contenant ses chiffres, à condition de savoir en quelle base est cette représentation :

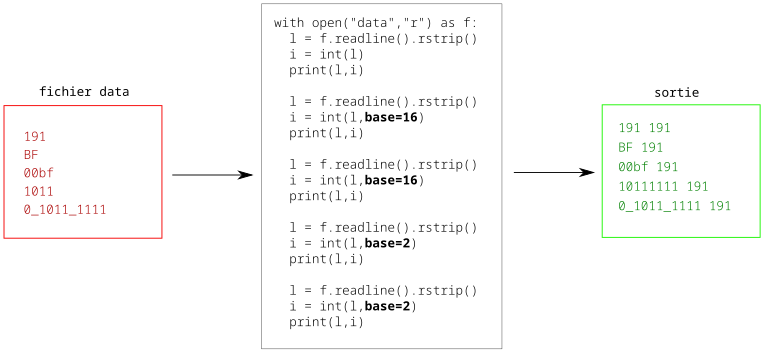
3.3. Fichier binaire

Lorsque l’on stocke des données dans un fichier, on peut vouloir que ce fichier soit lisible par un humain sans super-pouvoir. On génère donc un fichier texte.

Ecrire des nombres dans un fichier, avec par exemple print(…, file=…), les formate pour être humainement compréhensibles. Par exemple, écrire de cette façon l’entier représenté par les 4 octets 00 00 00 64 donne les 3 caractères '1', '0', '0' (puisque 00 00 00 64 est la représentation binaire de 100).

Au contraire, on peut vouloir réaliser une recopie brute, sans formatage donc plus rapide, de ces entiers. On obtient alors dans le fichier une copie conforme de la mémoire (la même suite d’octets, à l’ordre près), mais le fichier obtenu est dans ce cas un fichier binaire, incompréhensible par un humain (sans super-pouvoir).

3.3.1. Exemple pour des entiers

création d’un fichier binaire

with open("/tmp/f.bin", "wb") as f: (1)
  for i in range(32768):
    f.write(i.to_bytes(2,"little"))

1	noter le `'b'`

lecture de ce fichier binaire

with open("/tmp/f.bin", "rb") as f:
    while True:
      i = f.read(2)
      if len(i)<2: break
      print(int.from_bytes(i,"little"), end=" ")

3.3.2. Cas général

Les exemples précédents utilisent les méthodes from_bytes() et to_bytes() du type int . Ils ne sont pas généralisables à d’autres types numériques.

La fonction pack du module struct convertit des données binaires en séquence d’octets au format interopérable, ce qui est indispensable pour lire des données binaires issues de tous horizons (sondes, séquenceurs, de programme non Python, etc.). Et inversement, on reforme la donnée initiale avec la fonction unpack.

Soit l’exercice consistant à socker les termes de la suite de Fibonacci inférieurs à une certaine valeur dans un fichier binaire.

Version 1: Pour l’écriture, on calcule un terme et on l’écrit dans la foulée :

from struct import pack

last = 100000
a = b = 1
with open("/tmp/fib1.bin", "wb") as f:
  f.write(pack("i",a))
  while (b<last):
    f.write(pack("i",b))
    a,b = b,a+b

Pour la relecture, ne connaissant pas le nombre d’entiers dans le fichier, on récupérera les entiers un par un.

Version 2: On stocke les termes dans une liste, que l’on écrit, en une seule instruction, dans le fichier :

from struct import pack

l = []
last = 100000
a = b = 1
l.append(a)

while (b<last):
  l.append(b)
  a,b = b,a+b
nb = len(l)

with open("/tmp/fib2.bin", "wb") as f:
  f.write(pack("i",nb))  (1)
  f.write(pack(f"{nb}i",*l))

1	on stocke le nombre d’entiers, pour faciliter les futures relectures.

4. Les flottants

La norme IEEE-754 définit le format des nombres à virgule flottante. Elle offre un format interopérable pour représenter (de façon approximative) les nombres réels.

Dans cette norme, un réel est d’abord mis sous la forme 1,kkkkkkkk x 2ⁿ, kkkkkkkkk étant la mantisse et n l’exposant. Puis sont mémorisés son signe (1 bit) son exposant (8 bits), et sa mantisse (23 bits).

Cette représentation est approximative. Pour s’en convaincre, il suffit de calculer par exemple 1.1 + 2.2 ou bien 0.1 + 0.1 + 0.1 - 0.3.